Electrons have two fundamental physical properties, their charge and spin. The charge of electrons has been discovered and carefully measured long time ago[1]. The utilization of the electron charge can be found in all electronic devices. The manipulation of the electron spin, on the other hand, has been proved to be more challenging because of its quantum mechanical nature. To elucidate the physics and to design applications of the electron spin, a research area named spintronics has been established, and its rapid advance has identified the essential role of the electron spin in many fundamental properties of condensed matter systems such as the spin Hall effect[2] and the quantum spin Hall effect[3]. In addition, the research on the electron spin has resulted in numerous applications such as the giant magnetoresistance structures and tunneling magnetoresistance devices[4].
Due to the spin-orbital coupling, the spin Hall effect can convert a charge current into a spin current. The charge-to-spin conversion is particularly of interest in nanostructures because in modern electronics functional structures are typically on the scale of a few nanometers.
There are two widely accepted methods in the spintronics community to analyze experimental data for extracting the charge-to-spin conversion efficiency. Both methods rely on the model previously developed for thin film geometries[5]. One method focuses on the ratio of the amplitudes of the Lorentzian peak and the anti-Lorentzian peak, and therefore is defined as the lineshape method; while the other extracts the desired information by analyzing the linewidth of the measured signal peaks and is referred to as the linewidth method. Both approaches have been routinely applied to microstructures, the structures that are on the scale of microns (1 micron = 1000 nanometer). Recently, the research, published in Physical Review Applied titled "Charge-To-Spin Conversion Efficiency in Ferromagnetic Nanowires by Spin Torque Ferromagnetic Resonance: Reconciling Lineshape and Linewidth Analysis Methods" by Jun-Wen Xu and Prof. Andrew D. Kent from New York University, USA, demonstrated that when the lineshape and the linewidth methods derived from the thin film model were applied to nanostructures, they generated nonphysical results[6]. To address, the NYU group developed a novel model for nanowires and verified by micromagnetics that when experiments are analyzed with the new model, both analysis methods led to consistent and correct results. The nanowire model was developed based on the observation that when the width of a nanowire was below certain threshold, the in-plane magnetic anisotropy, the direction of the magnetization at its equilibrium state and the Oersted field should all be included properly. The conventional thin film model, however, fails to capture all the aforementioned details and therefore gives rise to incorrect results for nanostructures[6].
To confirm the effectiveness of the nanowire model, the group from New York University employed the spin torque ferromagnetic resonance (ST-FMR) technique. The implementation of ST-FMR requires multilayer thin film structures consisting of a magnetic layer and a conducting layer formed by heavy elements. The samples used in this work were synthesized by magnetron sputtering in a Kurt J Lesker Lab Line 12 system with the base pressure of 5×10-9 Torr (see Figure 1). Multilayer stacks Ta(3)/Py(5)/Pt(6) were prepared on Si substrates with thermally oxidized SiO2 top layers. (The numbers in the parenthesis indicate the thickness of each layer in nanometers.). The 3 nm Ta layer was prepared directly on top of the substrate as a seed layer. Because of the strong bonding of Ta ions to oxide surfaces and to the strong metallic bonding between Ta and other transition metals, a thin layer of Ta is known to be effective for serving as an adhesion and smoothing layer, reducing the grain size of subsequent layers [7]. Permalloy (Py) is a ferromagnetic metal and has the chemical composition of Ni80Fe20. The Py layer offers spontaneous magnetization for ferromagnetic resonance measurement. The platinum (Pt) is a heavy element with strong spin-orbit coupling. Therefore, the Pt layer allows charges to be converted into spins that exert a torque onto the magnetization in the Py layer making it precess. When the frequency of the precession is equal to the frequency defined by the experimental setup, a resonance occurs and can be picked up by monitoring the voltage cross the nanowire. More detailed discussion about ST-FMR can be found in Ref. [6, 8]. After deposition, electron beam lithography and argon ion milling were exploited to define the nanowire structures. The nanowire samples investigated in this work have various width (from 150 nm to 800 nm) with a fixed aspect ratio of 20[6].

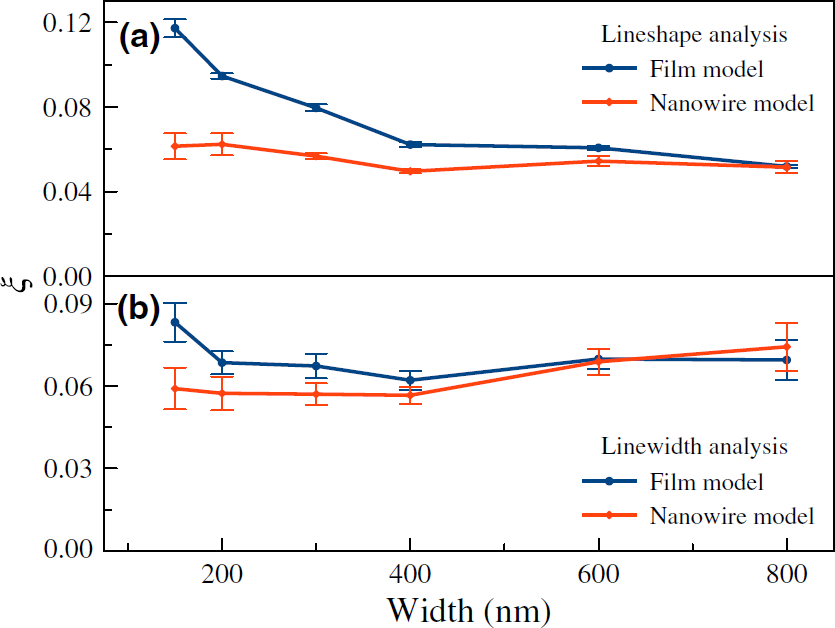
The analysis on the data revealed that when the conventional thin film model was applied, by using the lineshape method, one found that the charge-to-spin conversion efficiency clearly depended on the width of the nanowires. (See the blue line in Fig. 2 (a).) The same trend was also observed by using the linewidth analysis. (See the blue line in Fig. 2 (b).) The dependence of the charge-to-spin conversion efficiency on the width of the nanowire was not physical because it is an intrinsic property of Py/Pt interface and all the samples were made of the same materials. In comparison, when the new nanowire model was applied, both the lineshape (the red curve in Fig. 2 (a)) and the linewidth analysis (the red curve in Fig. 2 (b)) gave reasonable results: The charge-to-spin conversion efficiency was almost identical for all the samples with different widths. Furthermore, the comparison on parameters such as gyromagnetic ratio and the micromagnetic simulations both corroborated the validity of the nanowire model[6]. In further steps, the group from New York University is interested in extending the model to other nanostructures with different types of magnetic order.
References
- T. Arabatzis, "Representing Electrons: A biographical Approach to Theoretical Entities", University of Chicago Press (2006)
- J. Sinova, S. O. Valenzuela, J. Wunderlich, C. H. Back and T. Jungwirth, "Spin Hall Effects", Rev. Mod. Phys. 87, 1213 (2015)
- M. Z. Hasan and C. L. Kane, "Colloquium: Topological Insulators", Rev. Mod. Phys. 82, 3045 (2010)
- M. Wang, Y. Zhang, X. Zhao and W. Zhao, "Tunnel Junction with Perpendicular Magnetic Anisotropy: Status and Challenges", Micromachines 6, 1023 (2015)
- L. Liu, T. Moriyama, D. C. Ralph and R. A. Buhrman, Phys. Rev. Lett. 106, 036601 (2001)
- J. -W. Xu and A. D. Kent, "Charge-To-Spin Conversion Efficiency in Ferromagnetic Nanowires by Spin Torque Ferromagnetic Resonance: Reconciling Lineshape and Linewidth Analysis Methods", Phys. Rev. Appl. 14, 014012 (2020)
- J. M. Shaw, H. T. Nembach, T. J. Silva, S. E. Russek, R. Geiss, C. Jones, N. Clark, T. Leo and D. J. Smith, Phys. Rev. B 80, 184419 (2009)



